domingo, 27 de noviembre de 2011
lunes, 21 de noviembre de 2011
Bloque IX y X : Ecuaciones cuadraticas


APLICACIONES:
Tipo ax2 -c = 0
Despejamos el valor de x = √ c /a y obtenemos dos valores para x1 y x2
Consideremos que si c/a es menor que 1 no habrá solución y si es mayor que 1 obtendremos: x1 y x2
Ejemplos a solucionar:
1. 7x2 -49 = 0
2. 3x2 -9 = 0
3.10x2 -50 = 0
4. 10x2 -2 = 0
5. 36x2 -6 = 0
6. x2 -3 = 0
7. x2 -10 = 0
8. 8x2 + 16 = 0
9. 4x2 + 8 = 0
10. x2 -1 = 0
11. 2x2 + 2 = 0
12. x2 - 5 = 0
13. 25x2 -5 = 0
14. 3x2 -18 = 0
15. 2x2 -10 = 0
Al graficar una de las ecuaciones anteriores obtendremos los valores solución que será iguales, pero uno positivo y otro negativo, donde se intersecta la parábola en el eje de las x

Vertice= ( h, k)
h= -b/2a k= (4ac- b2 ) / (2a)
Tipo ax2 = 0
Ejemplos a solucionar:
1. 7x2 = 0
2. 3x2 = 0
3.10x2 = 0
4. -10x2= 0
5. 36x2 = 0
6. x2 = 0
7. -8x2 = 0
8. 8x2 = 0
9. -4x2 = 0
10. 3x2 = 0
Al graficar una de las ecuaciones anteriores obtendremos los valores solución que será cero, donde se intersecta la parábola en el eje de las x

Cuado la solución da x1 = 0 y x2 = ...un valor, si factorizados con término común.
Ejemplos a solucionar:
1. 4x2 - 8x = 0
2. x2 + 2x = 0
3. 4x2 - 5x = 0
4. x2 + x = 0
5. x2 + 5x= 0
6. x2 + 3x = 0
7. 4x2 - 20x = 0
8. 49x2 - 14x = 0
9. x2 - 6x = 0
10. 25x2 + 10x = 0
Al graficar nos da un valor x=0 y x= ... un valor dos valore para x

Completa: Tipo ax2 + bx + c = 0
Este caso se puede factorizar para encontrar el valor de x1 y x2 o solucionar por fórmula general.
1.- Por Factorización:
Ejemplo: y = - x2 -2 x + 3 a=-1, b= -2, c= 3
Vertice= ( h, k)
h= -b/2a k= (4ac- b2 ) / (2a)
Tipo ax2 + bx = 0
Ejemplos a solucionar por factorizacón:
1.
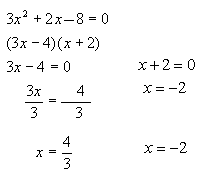
1. x2 + 4x + 4= 0
2. x2 + 3x - 54= 0
3. 4x2 - 5x -14 = 0
4. x2 + x - 42= 0
5. x2 + 5x -14 = 0
6. x2 + 3x - 54= 0
7. 4x2 - 20x + 25 = 0
8. 49x2 - 14x +1= 0
9. x2 - 6x -7 = 0
10. 25x2 + 10x + 1 = 0
2.- Por Formula General:

Ejemplo: y = - x2 -2 x + 3 a=-1, b= -2, c= 3

Ejemplos a solucionar por fórmula general y graficalas:
Nota para calcular el vértice (h.k)
h= -b/(2a) k= (4ac-b2)/(4a), esto para saber que valores le daremos al punto máximo o mínimo de la parabola.
1. x2 + 2x + 1= 0
2. x2 - 4x +3 = 0
3. - x2 + x + 6 = 0
4. x2 - 8x + 15 = 0
5. x2 + 2 = 0
Forma de graficar una ecuación cuadratica:

Vertice de parabola
Vertice= ( h, k)h= -b/2a k= (4ac- b2 ) / (2a)
Al graficar nos da un valor x=... un valor y x= ... un valor dos valores diferentes para x

Tipos de Parabolas
 Observa que es la misma ecuaución solo cambia el signo.
Observa que es la misma ecuaución solo cambia el signo.
Nota que entre má grande sea el número que acompaña a la variable cuadratica es menos ancha la parabola, y entre mas pequeño el numero de x 2 es mas ancha la parabola.
 Parabola sin solución ya que nunca intersecta con el eje de las x.
Parabola sin solución ya que nunca intersecta con el eje de las x.
Si tenemos y = x2 -1 significa que -1 baja la parabola, o y = x2 + 3 es lo que sube la parabola.
Vertices de la parabola

 Aquí el vertice (0,0)
Aquí el vertice (0,0)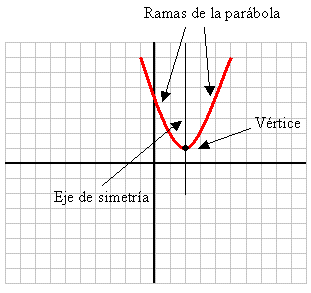
Parabola en su expresión canonica o cuando se presenta y = a(x - h)2 +k
para descubrir el valor del vétice ( h , k ) Conclusiones de parabolas:
El video siguiente solo es para aquel alumno que quiera aprender mas referente a completer el Trinomio Cuadrado Perfecto

lunes, 14 de noviembre de 2011
Bloque VIII
BLOQUE VIII.
Ecuaciones lineales II.
Previo. Al finalizar el bloque VII se encarga realizar una investigación sobre las características y propiedades de un sistema de ecuaciones simultaneas de 3 incógnitas.
Situación didáctica que debes contestar como diagnóstico.
Patricia, Juan y Rebeca salieron juntos a comprar postres para sus familias. Patricia compro 2 bolsas de dulces, 5 pastelillos y 2 gelatinas; Juan compro 1 bolsa de dulces, 10 pastelillos y 3 gelatinas; Rebeca compro 1 bolsa de dulces, 3 pastelillos y 5 gelatinas. Patricia pago $112, Juan pago $138 mientas que Rebeca pago $104. Héctor amigo de ellos quiere comprar 1 bolsa de dulces, 4 pastelillos y 4 gelatinas. ¿Cuánto debe pagar?
1) Plantea el sistema de ecuaciones de acuerdo a la situación anterior.
2) ¿Qué métodos de solución de ecuaciones lineales crees que debas de usar para resolver esta actividad?
3) ¿Qué información se complementa con los métodos anteriores?
4) ¿Hay más datos que incógnitas, más incógnitas que datos o el mismo número de incógnitas y datos?
5) ¿Qué dificultades se presentan al resolver la actividad?
Mario Bros en dos dimensiones
Mario Bros Tercera dimensión
Anexo 1: Se agrega la liga de un sistema de 3 x 3 por el método de determinantes.
Anexo 2: Otro método para resolver sistemas de tres ecuaciones lineales.
Anexo 3: Video para mostrar la solución de un sistema de tres ecuaciones lineales.
COLEGIO DE BACHILLERES DEL ESTADO DE CHIHUAHUA
PLANTEL – 1 T.M. SEMESTRE 2011 B
MATEMATICAS I
BLOQUE VIII
ELABORADO ING. CARMEN LETICIA ORTEGA NUÑEZ
FECHA:__________________
NOMBRE_____________________________________________GRUPO__________NL________
A CONTINUACION SE PRESENTAN DOS EJERCICIOS DE ECUACIONES LINEALES, RESUELVE UN EJERCICIO POR MEDIO DEL METODO ALGEBRAICO DE REDUCCION Y EL OTRO EJERCICIO POR MEDIO DEL METODO DE DETERMINANTES.
a) x+y+z=6
x-y+z=5
x+y-z=2
b) En cierta fabrica anexa al Plantel 1 de COBACH, se detecto que tres maquinas producian refrescos de 2lts. con falta de liquido. el primer dia la maquina A produjo 20 refresco, la maquina B, 10 y la maquina C 30. Ese dia la ganancia promedio por producto fue de $7. El segundo dia la maquina A produjo 10 refrescos; la B 20 y la C 20. La ganancia promedio ese dia fue de $1 por producto. El tercer dia la maquina A produjo 10 refrescos; La B, 20 y la C, 50. La perdida promedio reportada ese sia fue de $3 por producto. ¿Cuál de las tres maquinas habra que cambiar?
LISTA DE COTEJO PARA EVALUACION DE EJERCICIO DE BLOQUE VIII.
INDICADOR
|
2
|
0
|
Resolvió los dos ejercicios.
| ||
Planteo correctamente las ecuaciones del ejercicio b.
| ||
Cada uno de los ejercicios se resolvió por un método diferente.
| ||
Es correcto el resultado obtenido al menos para 1 ejercicio.
| ||
TOTAL
| ||
SI = 2 NO = 0
De acuerdo al los puntos obtenidos asigne el porcentaje de esta actividad.
Evaluación
| ||||||
Puntos obtenidos
|
0
|
2
|
4
|
6
|
8
| |
Porcentaje/Calificacion que se asigna
|
0
|
2.5
|
5
|
7.5
|
10
| |
miércoles, 2 de noviembre de 2011
bloque VII
REALIZA ECUACIONES LÍNEALES II
ACTIVIDAD PREVIA (EXAMEN DE DIAGNOSTICO)
EXAMEN DE DIAGNOSTICO
ECUACIONES SIMULTANEAS CON DOS INCOGNITAS
Resuelve cada una de las siguientes cuestiones y escribe en el paréntesis de la derecha la letra del inciso que contiene la respuesta correcta.
1. Al despejar “y” de la ecuación 2x + 5y = 9, la expresión que se obtiene es: ( )
a) 9 – 2x b) 2x – 9 c) 5( 9 – 2x) d) 9-2x
5
2. Al despejar “x” de la ecuación
a) 4y – 9 b) 8y – 9 c) 8y – 18 d) – 4y - 18
3. De la ecuación 2x – y + 3z = 11, los valores de las incógnitas son: ( )
a) 5, 1, 1 b) 6, 2, c) 4, 1 ,2 d) 3,– 2, 1
4. De la ecuación 3x – 5 = 4, el valor de la incógnita es: ( )
a)
5. Ecuación equivalente a x + 3y = 7 ( )
a) x + 4y = 9 b) 2x + 3y = 7 c) x – 3y = – 7 d) 2x + 6y = 14
6. Del sistema de ecuaciones
a) ( 4 , 3 ) b) ( 5 , 2 ) c) ( 2, 5 ) d) ( 7 , 3)
ACTIVIDAD DE INDAGACION
Investiga lo relacionado con las características y propiedades de un sistema de ecuaciones simultáneas de dos incógnitas.
SOLUCION DE UN SISTEMA DE DOS ECUACIONES CON DOS INCOGNITAS (2X2) MEDIANTE LAS GRAFICAS DE FUNCIONES LINEALES


Grafica de dos ecuaciones Tabulación para una gráfica
con dos incógnitas
Un sistema de ecuaciones simultáneas es aquel en el que el valor de cada variable es el mismo en cada ecuación que lo integra.
con dos incógnitas
Un sistema de ecuaciones simultáneas es aquel en el que el valor de cada variable es el mismo en cada ecuación que lo integra.
De manera particular, si en un sistema simultáneo de dos ecuaciones de primer grado con dos variables, x y y, se obtiene un par de valores que satisface las dos ecuaciones, se dice que se tiene una solución del sistema. Si dicha solución es única, entonces se puede obtener por alguno de los métodos tratados en esta unidad.
Gran cantidad de problemas se pueden resolver a partir de su planteamiento como un sistema simultáneo de dos ecuaciones con dos variables.
IDENTIFICAR SI UN SISTEMA 2X2 POSEE UNA, NINGUNA O INFINITAS RESOLUCIONES
La solución del sistema es el par de coordenadas que corresponde al punto común de las dos rectas, es decir, su punto de intersección.

Caso a) CONSISTENTE. Una solución, donde se intersectan las dos lineas de las dos ecuaciones
Caso b) Un número infinito de soluciones, porque se enpalman las lineas de las dos ecuaciones
Caso c) INCONSISTENTE. Las dos lineas son paralelas, indicando que nunca se unirán y no tiene solución este sistema de ecuaciones

ACTIVIDAD DE ANALISIS Y REFLEXION (explicar en clase)
1) Resuelve gráficamente el sistema formado por las ecuaciones x+2y=7 , 2x-y= -1.
y= 7-y y= 2x+1
2
(x,y) (x,y)
A(1,3) D(-1,-1)
B(3,2) E(0,1)
C(5,1) F(1,3)
Solución:
x=1
x=3
Este sistema está formado por dos ecuaciones simultáneas e independientes.
Cuando un sistema como el anterior tiene una solución, se dice que es compatible, consistente o determinado.
2) Resuelve gráficamente el sistema formado por las ecuaciones x+y=3 , x+y=5.
y=3-x y=5-x
(x,y) (x,y)
A(1,2) D(1,4)
B(0,3) E(0,5)
C(-1,4) F(3,2)
El ejemplo anterior representa un sistema sin solución, por consiguiente, es incompatible. Como representación de las ecuaciones corresponde a dos rectas que no se cortan.
En este ejemplo el sistema está formado por dos ecuaciones independientes, pero no son simultáneas ya que las variables no tienen el mismo valor.
En la primera ecuación y=3-xy en la segunda y=5-x.
SOLUCION DE UN SISTEMA DE DOS ECUACIONES CON DOS INCOGNITAS (2X2)

Para resolver un sistema de éste tipo se utilizan diversos métodos algebraicos como los siguientes:
· Eliminación por sustitución
· Eliminación por igualación
· Determinante
· También se utiliza el método gráfico.
A continuación se explica cada uno de estos métodos con el propósito de aplicarlos a la resolución de problemas.
Métodos algebraicos
Método de eliminación por reducción
A éste método se le conoce como de reducción por suma o resta. El procedimiento consiste en realizar las transformaciones necesarias con las ecuaciones para obtener una sola ecuación con una variable. A este proceso se le llama eliminación, pues mediante multiplicaciones adecuadas se igual el valor absoluto de los coeficientes de una misma variable en ambas ecuaciones y después se suman o restan miembro a miembro para eliminar dicha variable.
ACTIVIDAD DE ANALISIS Y REFLEXION
- Cuando los coeficientes de la variable a eliminar son iguales en valor absoluto. Halla dos números tales que su suma sea 7 y su diferencia 1.
Solución:
Sean x y y los números que se buscan.
El problema se puede plantear con el siguiente sistema.
x+y=7… (1)
x-y=1… (2)
la variable y se puede eliminar si se suman miembro a miembro las ecuaciones (1) y (2), es decir:
x+ y= 7
x- y= 1
2x =8
De donde:
x= 8
2
x= 4…(3)
Sustituyendo (3) en (1) se obtiene: x + y= 7
4 + y= 7
Por tanto: y= 7- 4
y=3
Comprobación:
Se sustituyen las dos variables por los valores hallados:
x+ y =7…(1) x- y =1…(2)
4+ 3 =7 4- 3 =1
7=7 1=1
- Cuando los coeficientes de las variables a eliminar son diferentes en valor absoluto.
Por 5 plumas y 3 lapiceros se pagaron 136 unidades de dinero, y por 3 plumas y 4
lapiceros se pagaron 108 unidades de dinero.
Halla el valor de cada pluma y de cada lapicero.
Solución:
Si se presentan las plumas por p y los lapiceros por l, el problema se puede plantear
Con el siguiente problema:
5p+3l=136… (1)
3p+4l=108… (2)
Si queremos eliminar la variable p, se requiere que sus respectivos coeficientes sean
iguales en valor absoluto. Esto se consigue si la ecuación (1) se multiplica por 3 y la
ecuación (2) se multiplica por 5 para obtener las ecuaciones equivalentes (3) y (4).
3(5p+3l = 136)
5(3p+4l = 108)
15p+9l = 408…
15p+20l = 540…
La variable p se elimina restando mimbro a miembro la ecuación (4) de la (3) es decir:
15p+9l = 408
15p+20l = 540
-11l = -132
de donde:
l = -132
-11
l = 12…(5)
El valor de p se obtiene al sustituir (5) en cualquiera de las ecuaciones del sistema
Original o del sistema transformado.
Sustituyendo (5) en (1) se obtiene: 5p+3l = 136
5p+3(12) = 136
5p+36 = 136
5p = 136-36
5p = 100
p = 100
5
p = 20
Comprobación:
Se sustituyen las dos variables por los valores hallados:
5p+3l = 136… (1) 3p+4l = 108… (2)
5(20) + 3(12) = 136 3(20) + 4(12) = 108
100+36 = 136 60+48 = 108
136 = 136 108 = 108
Método de eliminación por sustitución
El proceso consiste en despejar una variable en una de las ecuaciones. La expresión asì obtenida se sustituye en la otra ecuación para obtener una nueva ecuación con una sola variable. Se encuentra el valor de ésta y se sustituye en la expresión despejada de la otra variable para determinar su valor.
ACTIVIDAD DE ANALISIS Y REFLEXION
1) Para un espectáculo se vendieron 300 boletos de 20 y 30 unidades de dinero. ¿Cuántos
boletos se vendieron de cada precio si el total de venta fue de 8000 unidades de
dinero?.
Solución:
Sean x y y el número de boletos de 20 y 30 unidades de dinero, respectivamente.
entonces:
x+y = 300… (1)
20x+30y = 8000… (2)
Despejando y en (1): x+y = 300
y = 300-x… (3)
Sustituyendo (3) en (2):
20x+30y = 8000
20x+30(300-x) = 8000
Efectuando el producto indicado: 20x+9000-30x = 8000
Reduciendo términos semejantes: 9000-10x = 8000
Transponiendo términos: 9000-8000 = 10x
De donde: 1000 = 10x
Por tanto: 100 = x… (4)
Sustituyendo (4) en (3): y = 300-x
y = 300-100
y = 200
Comprobación:
x+y = 300… 819 (1) 20x+30y = 8000… (2)
100+200 = 300 20(100)+30(200) = 8000
300 = 300 2000+6000 = 8000
2) Un ganadero vendió 50 terneras y 220 ovejas por 16,150 unidades de dinero; con los
mismos precios vendió 40 terneras y 180 ovejas por 13, 100 unidades de dinero.
encuentra el precio de cada ternera y de cada oveja.
Solución:
Sea x el precio de cada ternera y y el precio de cada oveja. Por tanto:
50x+ 220y = 16150…
40x+180y = 13100…
Despejando y en (1): 50x+220y = 16150
220y= 16150-50x
y = 16150-50x …
220
Sustituyendo (3) en (2): 40x+180y = 13 100
40x+180 16 150-50x = 13 100
220
Multiplicando la ecuación por 220:
220[40x+180 16 150-50x = 13 100]
8 800x+180(161 50-50x) = 2 882 000
Efectuando operaciones y simplificando:
8800x+2 907 000-9000x = 2 882 000
2 907 000-2 882 000 = 200x
25 000 = 200x
25 000 = x
200
125 = x… (4)
Sustituyendo (4) en (3): y= 16 150-50x
220
y= 16 150-50(125)
220
y= 16 150-6 250
220
y= 9 900
220
y= 45
Por tanto, el precio de cada ternera es de 125 unidades de dinero y el de cada oveja es
de 45 unidades de dinero.
Método de eliminación por igualación
El proceso consiste en despejar la misma variable en las dos ecuaciones. Las expresiones así obtenidas se igualan para tener otra ecuación con una sola variable. Se encuentra el valor de ésta y se sustituye en la expresión despejada de la otra variable para determinar su valor.
ACTIVIDAD DE ANALISIS Y REFLEXION
- La suma de las edades actuales de una persona y su hijo es de 66 años. Determina sus edades sabiendo que dentro de tres años, la edad del padre será el triple de la edad de su hijo.
Solución:
Si se presentan con P y H las edades actuales del padre y su hijo, el problema se
plantea con el siguiente sistema:
P+H = 66… (1)
P+3 = 3(H+3)… (2)
Efectuando las operaciones indicadas en (2) y ordenando sus términos, el sistema nos
queda así:
P+H = 66… (3)
P+3 = 6… (4)
Si se quiere eliminar la variable P, se despeja ésta en (3) y (4).
De (3) P = 66 – H… (5)
De (4) P = 6+3H… (6)
Igualando (5) y (6) se obtiene 66 – H = 6+3H
Por lo que 66 – 6 = 3H+H
por tanto: 60 = 4H
de donde: 60 = H
4
osea: 15 = H (7)
El valor de P se obtiene al sustituir (7) en (5) o en (6),
Sustituyendo (7) en (5)
P = 66 – H
P = 66 –15
de donde : P = 51
Comprobación:
Se sustituyen las dos variables por sus respectivos valores en (1) y (2).
P+H = 66… (1) P+3 = 3(H+3)… (2)
51+15 = 66 51+3 = 3(15+3)…
66 = 66 54 = 3(18)
54 = 54
- El precio de una mezcla de dulces de una unidad de dinero el kilogramo con otros de 1.40 unidades el kilogramo es de 17 unidades de dinero pero si se toma el doble de dulces del segundo tipo, el precio d la mezcla es de 24 unidades de dinero.
Encuentra el número de kilogramo de cada tipo de dulces.
Solución:
Sean D el número de kilogramo de dulces del primer tipo y d el número de kilogramo
de dulce del segundo tipo.
El problema se puede plantear así:
100D+140d =1700… (1)
100D+140(2d) = 2 400… (2)
Al hacer la operación indicada en (2) el sistema queda así:
100D+140d = 1 700… (3)
100D+280d = 2400… (4)
Si se quiere eliminar la variable d, se despeja ésta en (3) y (4).
De (3)
140d = 1 700-100D
d = 1 700-100D... (5)
140
De (4)
280d = 2400-100D
d = 2400-100D … (6)
280
Igualando (5) y (6) se obtiene
1 700-100D = 2 400-100D
140 280
Aplicando la propiedad fundamental de las proporciones
280(1 700-100D) = 140(2 400-100D)
Se divide la igualdad entre 140
2(1 700-100D) = (2 400-100D)
Se suprimen paréntesis
3400-200D = 2400-100D
por tanto: 3400-2 400 = -100D+200D
o sea: 1000 = 100D
de donde 1000 = D
100
10 = D… (7)
El valor de d se obtiene al sustituir (7) en (5) o en (6).
Sustituyendo (7) en (5)
d = 1 700-100(10)
140
d = 1 700-1000
140
d = 700
140
d = 5
Comprobación:
Se sustituyen las dos variables por sus respectivos valores.
100D+140d = 1 700… (1) 100D+280d = 2 400… (2)
100(10)+140(5) = 1 700 100(10)+280(5) = 2 400
1000+700 = 1 700 1000+1400 = 2 400
1 700 = 1 700 2400 = 2 400
METODO NUMERICO POR DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES (2X2)
El símbolo
ordenados en una matriz de dos filas y dos columnas, representa un determinante de segundo orden o determinante de orden dos. Los seis números anteriores se denominan elementos de la matriz o del determinante.
Si las ecuaciones son: 4x + 2y = 52
x + y = 18
Así la solución del sistema será:

ACTIVIDAD DE ANALISIS Y REFLEXION
Resuelve el sistema:
3x+5y = 11 donde: a1 = 3 b1 = 5 c1 = 11
2x-y = 16 a2 = 2 b2 = -1 c2 = 16
Que son los coeficientes de x y y el término independiente.
Por lo tanto, sustituyendo nos quedaría que:
x = 7
y = -2
ACTIVIDAD DE APLICACIÓN DEL CONOCIMIENTO (Resolver en clase por equipos)
1) Resuelve los siguientes sistemas de ecuaciones por reducción.
x-3y = 11 5x - 8y = 8
4x-5y = 30 x + y = 12
2) Resuelve los siguientes sistemas de ecuaciones por sustitución.
4x-3y = 5 6x+3y = 8
2x+5y = -4 4x-6y = 8
3) Resuelve los siguientes sistemas de ecuaciones por igualación.
8x-5y = 9 10x-9y = 18
6x-7y = 10 2x+6y = 1
4) Resuelve los siguientes sistemas de ecuaciones por determinantes.
x-2y = 1 3x-2y = 2
x-3y = 3 2x+y = 8
5) Resuelve por el método que elijan y grafícalo.
8 litros de gasolina magna y 10 litros de gasolina Premium cuestan $82 pesos, mientras que 4 litros de gasolina magna y 7 litros de gasolina Premium cuestan $51 pesos. ¿Cuál es el precio por litro de cada tipo de gasolina?
ACTIVIDAD DE INTEGRACION (Tarea)
- Resuelve cada una de las siguientes cuestiones y selecciona el inciso que corresponda a la respuesta correcta.
1. La solución del sistema de ecuaciones x + y = 8 , x – y = 6 es ( )
a) (5, 3) b) (6, 2) c) (7, 1) d) (8, 0)
2. La solución del sistema de ecuaciones 2x – y = 6, x + y = 6 es ( )
a) (3, 0) b) (4, 2) c) (5, 1) d) (3, 0)
3. El punto P (2, 4) es común a ( )
a) b)
- Resuelve los siguientes problemas razonados que involucran un sistema de ecuaciones lineales con dos incógnitas.
- Si 12kg de papas y 6kg de arroz cuesta $102 pesos, mientras que 9kg de papas y 13kg de arroz cuestan $153 pesos ¿Cuál es el precio por kilogramo de cada producto?
- Guillermo invirtió parte de su dinero al 12% y el resto al 15%. El concepto de interés por ambas inversiones totalizo en $3,000 pesos. Si hubiera intercambiado sus inversiones el ingreso habría totalizado a $2,940 pesos. ¿Qué cantidad tendría en cada inversión?
3. Al ir corriente abajo un bote promedia una velocidad de 18km/h, al regresar a contra corriente su velocidad promedio es de 6km/h. ¿Cuál es la rapidez de la corriente del agua?
ACTIVIDAD DE APOYO
Conéctate a http://maralboran.org/wikipedia/index.php/Sistemas_de_ecuaciones_de_primer_grado y observa las gráficos distintos tipos de sistema de ecuaciones lineales.
Suscribirse a:
Entradas (Atom)
